在技术日新月异的今天, 当年一些看起来高大上的技术, 现在越来越白菜价了. 一个典型的例子是手写数字识别. 记得我刚上大学的时候, 身边还没多少人用微信, 群发消息还是用飞信. 那时要是谁可以写个手写数字识别的算法, 是一件挺令人羡慕的事. 毕竟那时Python库scikit-learn(sklearn)才刚刚发布, 更没人料到Python能在不久将来打下人工智能的半壁江山.

而今天, 人工智能已经烂大街了. 现在入门人工智能, 有两样是绕不开的, 一个是sklearn库, 另一个是机器学习的一个经典案例--手写数字识别.

下面我来讲讲怎么用sklearn库来实现手写数字识别.

必需强调, 这只是机器学习的敲门砖, 不是机器学习的终点.

导入数据

sklearn自带有一个小型的手写数字样本, 导入代码如下:

from sklearn.datasets import load_digits
x = digits.data    #数组化的手写数字样本, 每个都是长度为64的数组, 可以`reshape`成一张8*8的矩阵, 再通过plt.imshow 即可浏览原手写数字图片
y = digits.target  #与 x 相应的标签, 0-9.
x_train, x_test, y_train, y_test = train_test_split(x, y, test_size = 1/5,) #把样本随机分成训练集与测试集两部分, 其中测试集占1/5

下图是该手写数字样本的部分样例.

训练模型

把图片识别为0-9这10个数字, 这是一个分类问题. 这里采用的模型是支持向量机(Support Vector Machine, SVM). 之所以用这个, 是因为经验表明这个模型优于其他模型(包括神经网络). 这里不科普什么是支持向量机, 你知道它是个能用来分类的模型就行了.

用训练集中的数据训练模型, 代码如下:

from sklearn.svm import SVC
mdl = SVC(gamma=0.001)      #模型初始化, 这里的gamma=0.001是个经验值
mdl.fit(x_train, y_train)   #导入训练集的数据, 训练模型

模型检验

衡量一个模型的准确度有很多指标, 我一般采用准确度和混淆矩阵(confusion matrix, 数据越往矩阵对角线集中, 模型则越准确).

用测试集的数据检验模型, 代码如下:

confusion_matrix(y_test, mdl.predict(x_test))  #模型在测试集上的混淆矩阵
mdl.score(x_train, y_train)  #模型在训练集上的准确度
mdl.score(x_test, y_test)    #模型在测试集上的准确度

完整代码

以下是完整代码. 最后输出判断失误图片和程序运行时间.

from sklearn.datasets import load_digits
from sklearn.svm import SVC
from sklearn.metrics import confusion_matrix
from sklearn.model_selection import train_test_split
from time import time
import numpy as np
import matplotlib.pyplot as plt

np.random.seed(0)  #随机种子, 确保输出结果一样.

t0 = time()  #起始时间

digits = load_digits()

x = digits.data
y = digits.target

x_train, x_test, y_train, y_test = train_test_split(
        x, y, test_size = 1/5, )

# 训练模型
mdl = SVC(gamma=0.001)
mdl.fit(x_train, y_train)

# 模型在测试集上的混淆矩阵
print('Confusion matrix:')
print(confusion_matrix(y_test, mdl.predict(x_test)))

# 模型在训练集和测试集上的准确度
print('Score in training set: %1.3f.'%mdl.score(x_train, y_train))
print('Score in test set: %1.3f.'%mdl.score(x_test, y_test))

def digitshow(x, y):    #函数, 输出手写数字图片和相应的数字
    plt.figure(figsize=[.5,.5])
    plt.axis('off')
    plt.imshow(x.reshape(8,8), cmap=plt.cm.gray_r)
    plt.title(y)
    plt.show()

# 输出判断错误的图片
print('Error:')

for a, b in zip(x_test, y_test):
    p = mdl.predict([a])
    if p != b:
        digitshow(a, b)
        print('Predict = %d, true = %d'%(p[0],b))

print('Total Time = %1.1fs'%(time()-t0))    #程序运行时间

程序运行结果

Confusion matrix:
[[27  0  0  0  0  0  0  0  0  0]
 [ 0 35  0  0  0  0  0  0  0  0]
 [ 0  0 36  0  0  0  0  0  0  0]
 [ 0  0  0 29  0  0  0  0  0  0]
 [ 0  0  0  0 30  0  0  0  0  0]
 [ 0  0  0  0  0 39  0  0  0  1]
 [ 0  0  0  0  0  0 44  0  0  0]
 [ 0  0  0  0  0  0  0 39  0  0]
 [ 0  1  0  0  0  0  0  0 38  0]
 [ 0  0  0  0  0  1  0  0  0 40]]
Score in training set: 0.999.
Score in test set: 0.992.
Error: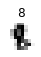

Predict = 1, true = 8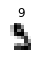

Predict = 5, true = 9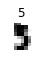

Predict = 9, true = 5
Total Time = 0.7s

运行结果出现了3个误判, 总的准确率为99.2% (357/360).